¿Qué es la simplificación de circuitos?
La simplificación de circuitos eléctricos resistivos nos ayuda a interpretar la ley de ohm, con mucho mayor facilidad, ya que para aplicar la formula de la corriente para un circuito necesitamos saber el valor de la resistencia y el voltaje del circuito.
Pero ¿Qué pasa cuando tenemos más de una resistencia?
Cuando tenemos más de un valor se dificulta todo el proceso, ya que esta formula solo esta diseñada para calcular la corriente con solo un dato de resistencia y uno de voltaje. Es aquí donde entra la simplificación de los circuitos, para obtener la resistencia total tenemos que ir reduciendo el circuito hasta quedarnos solo con el circuito básico que seria, una fuente de voltaje y una resistor.

Tipos de circuitos resistivos
Existen tres formas de agrupar los circuitos: En serie, en paralelo y mixtos. Estos últimos son la combinación de los dos primeros.
Circuitos en serie
Este tipo de circuitos se genera cuando las resistencias están unidas solo por una terminal (una detrás de la otra). Las características principales de estos circuitos es que la corriente siempre es la misma en todo el circuito y el voltaje va disminuyendo con cada resistencia. la formula para calcular estos circuitos es la suma de cada una RT= R1+R2+R3+…+Rn

Circuitos paralelo
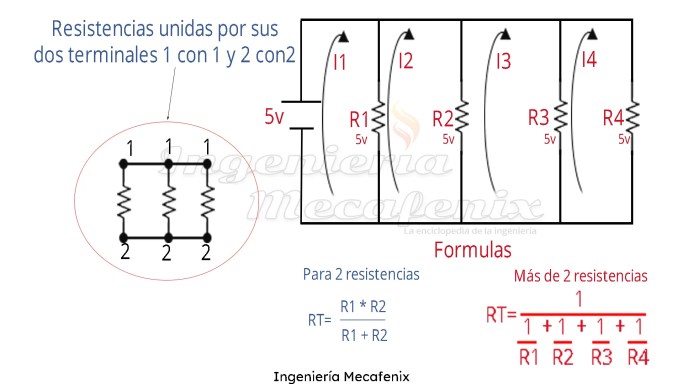
Las resistencias están unidas de la misma forma, la terminal 1 con la 1 y la 2 con la 2. La corriente y el voltaje dentro de estos circuitos funciona de manera inversa, ya que el voltaje que pasa por cada elemento es el mismo, pero la corriente se disminuye con cada resistor. Existen 2 formulas para estos circuitos cuando son solo 2 dispositivos en paralelo RT= R1 * R2 / R1 + R2 y cuando son más de dos RT= 1/ (1/R1 + 1/R2 + 1/R3 + … + 1/Rn).
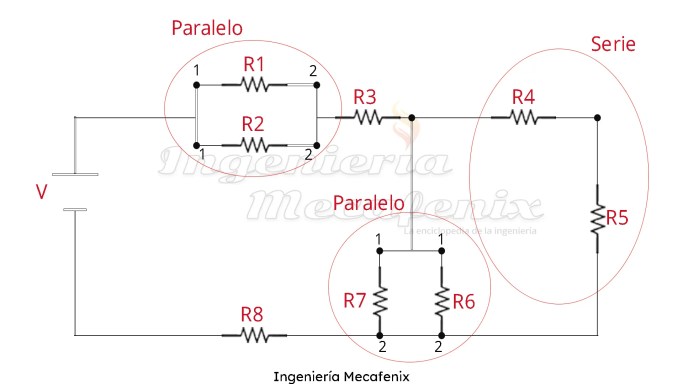
Circuitos mixtos
Estos circuitos son más complejos debido a que podemos encontrar resistencias en serie y en paralelo. Para la simplificación de este circuito se tiene que ir identificando que partes pueden resolverse primero y en que forma están.
Ejemplos
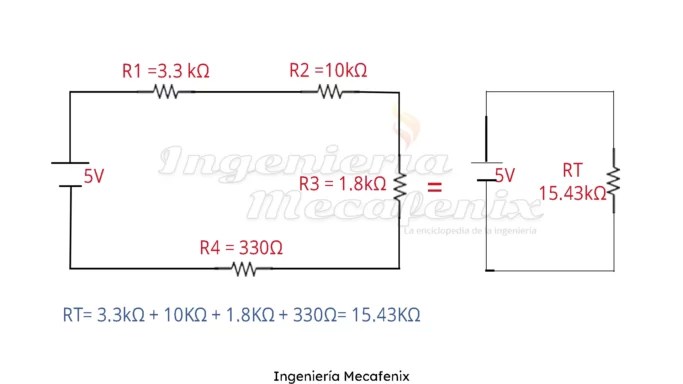
Circuito en serie
Este tipo de circuito es el mas sencillo ya que solo se suman los valores de las resistencias. lo único que tenemos que cuidar es cuando tenemos KΩ y Ω ya que 1KΩ=1,000Ω.
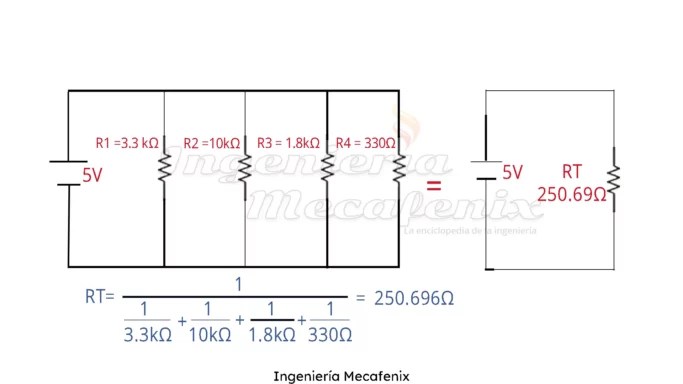
Circuito paralelo
Cuando es un circuito puramente paralelo no tiene mucha dificultad ya que solo utilizamos una formula, aun que siempre tenemos que estar atentos a los valores de las resistencias.
Circuito mixto
Para la simplificación de circuitos mixtos la dificultad puede aumentar o disminuir, ya que dependiendo el circuito algunos pueden estar más elaborados y más complejos y algunos otros pueden ser bastante sencillos. Recuerden observar bien los valores de las resistencias siempre.
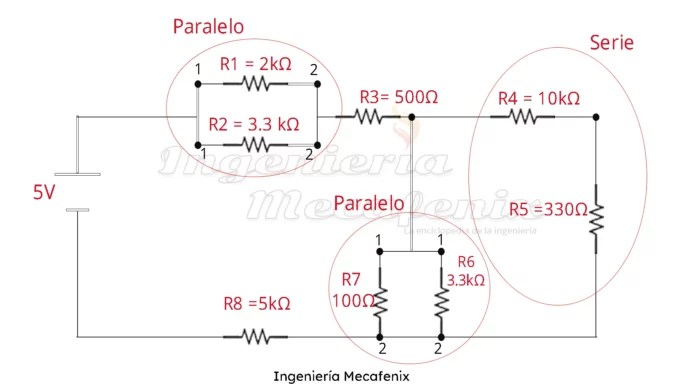
Una vez resueltos los primeros pasos, se sustituyen los resultados para seguir buscando posibles avances hasta llegar a la simplificación máxima. las R1,2 – R7,6 y R4,5 se manejan de esa forma para saber que el resultado provino de la simplificación de R1 y R2 o según sea el caso.

Por ultimo podremos darnos cuenta que todas la resistencias sobrantes quedaron en serie, solo basta con aplicar la formula para y logramos encontrar la resistencia total de circuito.

Una vez sacando la resistencia total y la corriente que circula por el circuito podemos sacar el voltaje de cada resistencia, la corriente que circula en cada malla, etc. (próximamente articulo sobre ese tema).
Artículos recomendados para ti
Si te gusto nuestro post no dudes en visitar nuestro otros artículos donde te explicamos los temas de una manera fácil y sencilla de entender




